Algorithms
uses a second order finite volume method to solve partial differential equations in the following conservative form \begin{align} \frac{\partial U}{\partial t} + \nabla\cdot F & = S \end{align} in a spatial volume with the boundary , where the conserved variables , the fluxes , and the sources are all functions of the primitive variables to be solved for, .
PDE evolution as a root finding problem
In , the time evolution of the above PDE is cast as a massive
nonlinear root finding problem, by re-writing it as
where are the primitive variables that need to be solved for, and
is a vector of the at every spatial
location in the discrete domain. The time evolution of the PDE then is a
question of what the roots of the above set of equations are. The
exact form of , and depend on the chosen temporal discretization scheme,
and are described in the temporal discretization section. The roots are obtained
by the Newton-Krylov algorithm, which only requires the residuals as
inputs. The Jacobian of the system needed for the nonlinear root finding is
assembled automatically with the input residuals.
The Newton-Krylov algorithm is summarized here. We want to solve
The unknowns are solved for by
where is the nonlinear Newton iteration index. The correction
is obtained by solving
where is the Jacobian of the system, whose sparsity
depends on the spatio-temporal scheme being used. The above linear system is
again solved iteratively using a preconditioned Krylov subspace method, namely
the Generalized Minimal RESidual method (GMRES). Thus, the procedure is a
nested iterative algorithm with the nonlinear Newton iteration at the other
level, and an inner Krylov iteration to solve for the correction . The Newton iteration is continued till , where
is a chosen norm and is the required tolerance.
The Newton-Krylov algorithm allows for flexibility with respect to the
underlying physical models because the sparse Jacobian is assembled efficiently
by finite differencing of the residuals,
where is a small parameter. uses the
Newton-Krylov implementation in the module of the
library1. The library detects the
connectivity between the elements based on our input discretization scheme and
estimates the sparsity of the Jacobian through graph coloring2, allowing for an
efficient assembly for both explicit and implicit time stepping schemes.
With the only inputs to the algoritm being the residuals, we now focus on the schemes involved in the residual assembly. The residuals are assembled by discretizing the above conservative equations using the finite volume formulation, where all the individual steps are detailed in later sections.
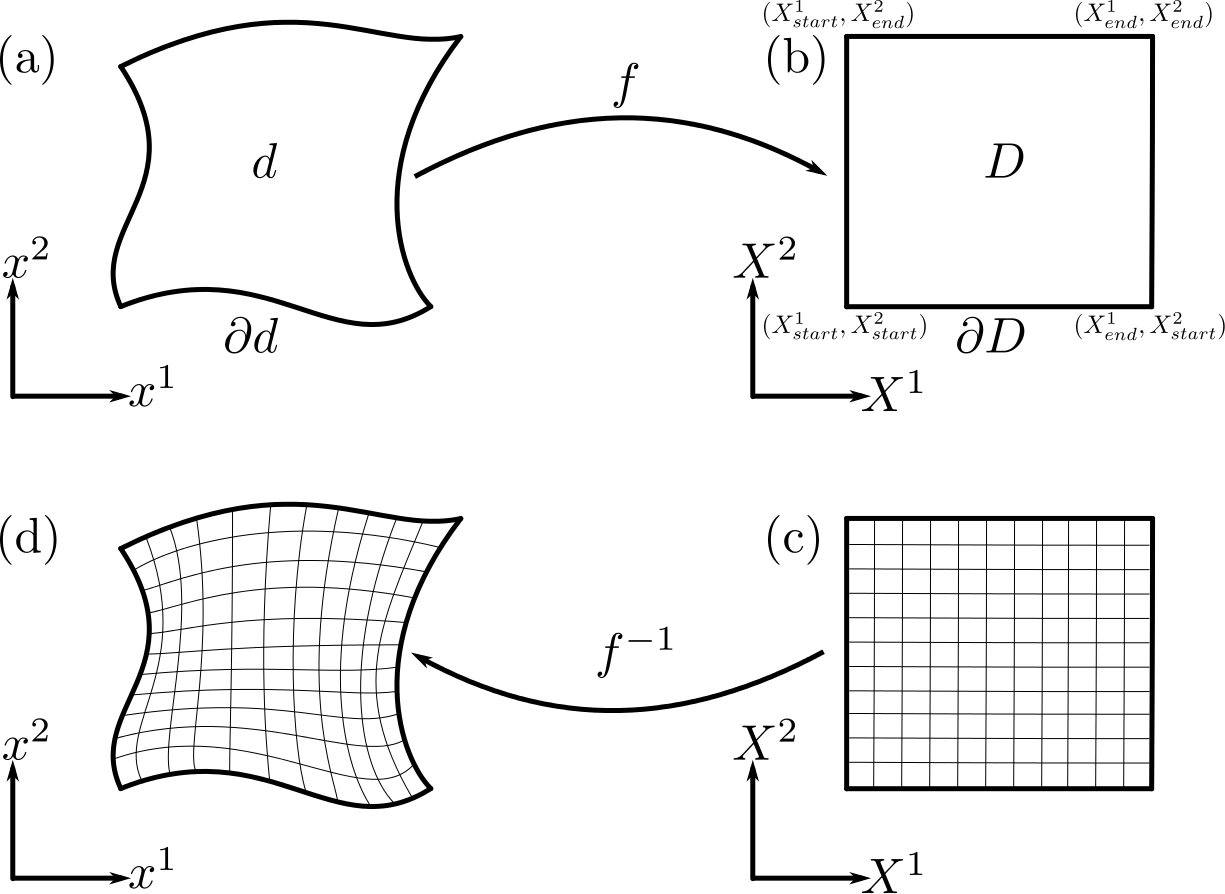
Grid Generation
The spatial volume , is discretized by transforming into a set of chosen
computational coordinates , in which the coordinate axes are aligned to
the transformed boundary . The boundaries are then simply defined
by a constant coordinate on all sides of the domain. The domain in these
coordinates is then discretized using a structured uniform hexahedral mesh.
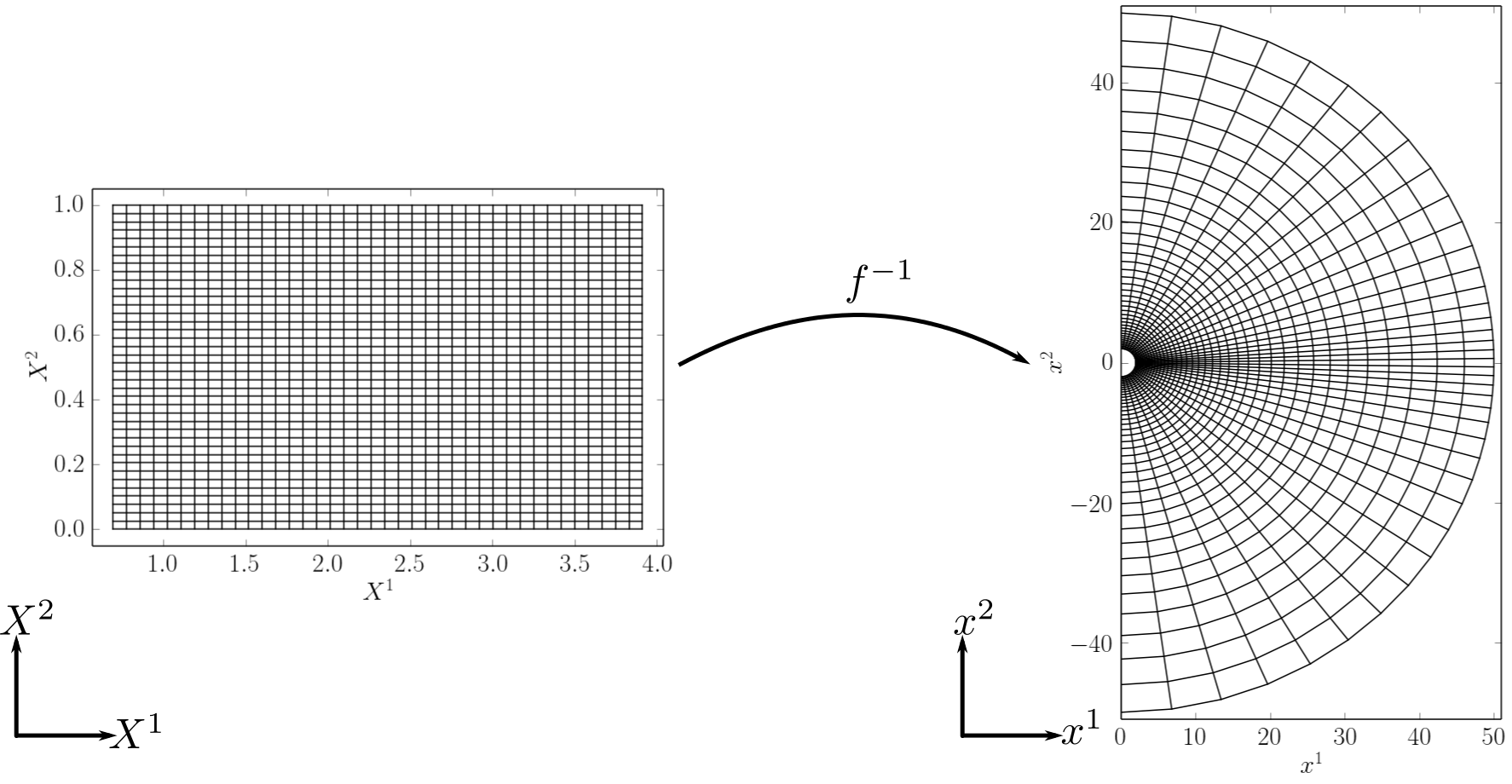
A common case involves discretizing spherical domains. This is used for example,
to study accretion flows. To construct a spherical mesh, a computational
coordinate system is chosen, which relates to the
cartesian coordinates by
where , and . With this coordinate mapping, a uniform grid in the coordinates
leads to an exponential packing () of the grid zones at the inner
boundary and a concentration of the grid zones at the midplane () which is controlled by the parameter .
The discretized domain is illustrated below for .
Finite Volume Method
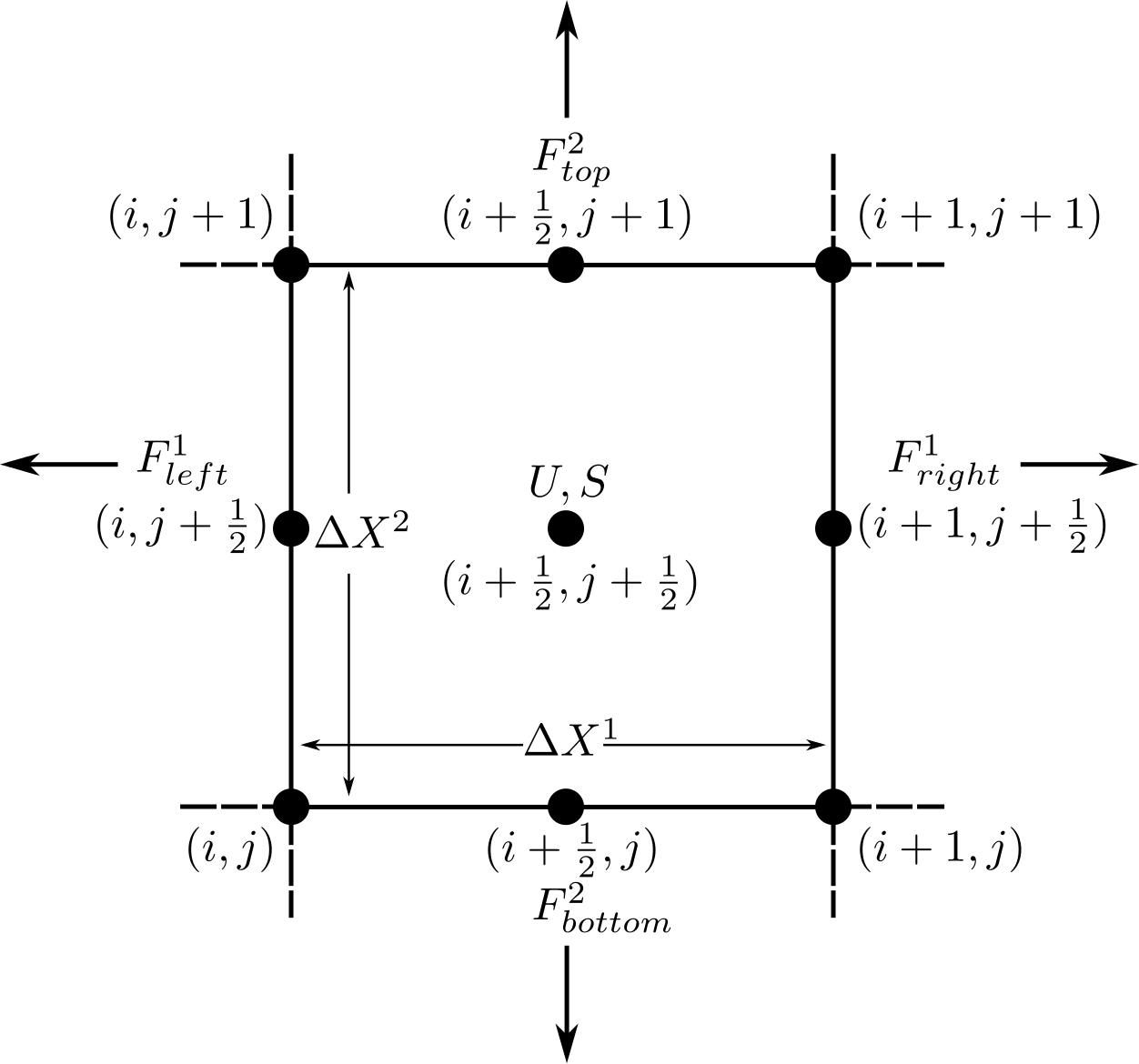
Muliplying the conservative equations by the volume element of a discrete grid zone
in the coordinate system, , and using the
divergence theorem leads to,
where , , , and . The locations , , and are
illustrated below for an individual grid zone. In , we denote
centers of the grid zones by half indices and faces by integer indices as
shown.
Temporal discretization
Multiplying further by , and performing the temporal integral over a discrete time interval gives
where the indices , and indicate the discrete time levels. The
volume integrals in , and the surface integrals in
are evaluated using a second order numerical quadrature, and
thus , and . For the temporal integrals and , can use any of the
following three schemes:
(1) Explicit time stepping:
- Fluxes :
- Sources :
The temporal half index indicates a half time step. This leads to
the following discrete equations
A complete time step for this scheme is performed in two stages. A half step , to solve for the primitive variables at the half step , which are then used to compute and . These are then used to perform a full step , thus completing the time integration over .
(2) IMEX Implicit-Explicit time stepping
- Fluxes (explicit) :
- Sources (implicit) :
This scheme is designed to handle the presence of stiff sources, by treating
them implicitly, while treating the flux terms explicitly. It leads to the
following discrete equations
The computation of the fluxes at the half step is the same as in the explicit scheme.
(3) Implicit time stepping:
- Fluxes : .
-
Sources :
This scheme is much more expensive than the explicit and imex schemes as will be described in the solver section. However, a fully implicit scheme has no Courant limits and is useful for testing new physics when the characteristics are not known accurately. The discrete equations are
Spatio-temporal derivatives in the source terms
The volume averaged source terms may contain spatio-temporal derivatives . Whenever present, the temporal derivatives in the source terms are approximated as , and the spatial derivatives are approximated using slope limited derivatives. The derivative of a quantity in the zone is computed from the values at the neighbouring points using , where in smooth flows and in the presence of discontinuities. The spatial derivatives of the required quantities are computed using the primitive variables at the half-step for the explicit and imex schemes, whereas it is a combination of the and steps for the implicit scheme.
Reconstruction
The finite volume method evolves the zone-averaged conserved variables , where . Therefore, the conserved variables and the primitive variables are located at zone centers , whereas the fluxes need to be computed at the , , and face centers . Thus, the need to reconstruct the values of the primitive variables to the zone faces. This is performed using a reconstruction operator which takes in primitive variables within a certain radius and constructs a polynomial interpolant from which the edge states can be computed. To achieve an error of , a linear interpolant is sufficient, for which the reconstruction operator has a stencil width of three grid zones. The operator can act in two directions depending on input order, whose output is the state , and , whose output is the state .
Illustrated below are the sequence of steps needed to compute and .
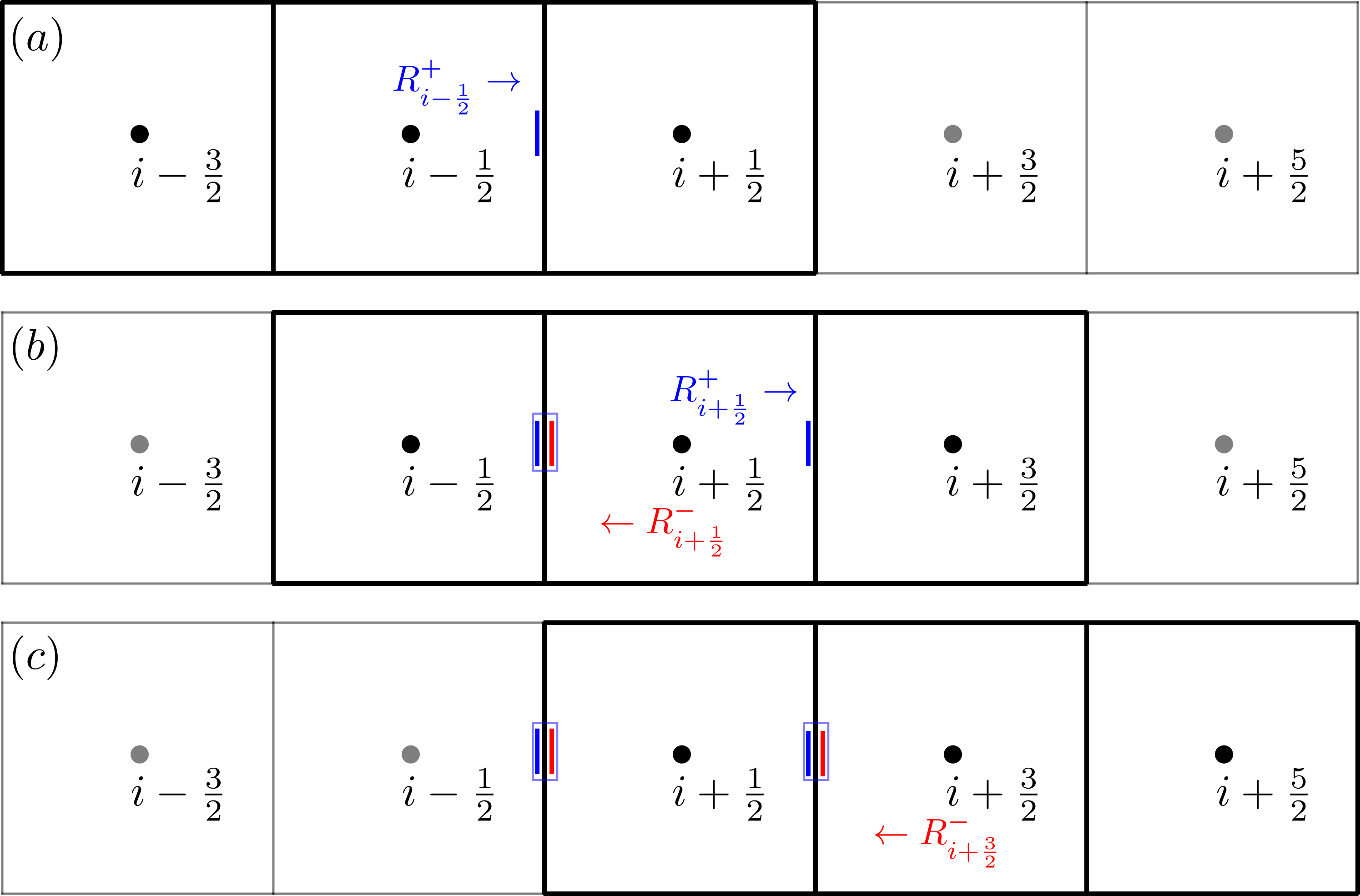
-
(a) Apply the operator to compute the primitive variables at the left side of the face (index = ).
-
(b) to compute the primitive variables at the right side of the face (index = ).
to compute the primitive variables at the left side of the face (index = ).
-
(c) to compute the primitive variables at the right side of the face (index = ).
After the reconstruction procedure described in the above sequence of steps, we have the primitive variables at the left and the right sides of the face and at the left and the right sides of the face. The fluxes at each face are then a function of the primitive variables at either side of the face, and . These are then computed using the Riemann solver.
The above procedure outlines the reconstruction in one-dimension. Since uses a structured mesh, the same one-dimension reconstruction operator along with the accompanying sequence of steps are followed to compute the edge states for the and faces.
Riemann solver
Given the left and right states on either side of a face, an approximate Riemann solver is used to compute the flux at the face. Shown below are the primitive variables after reconstruction.
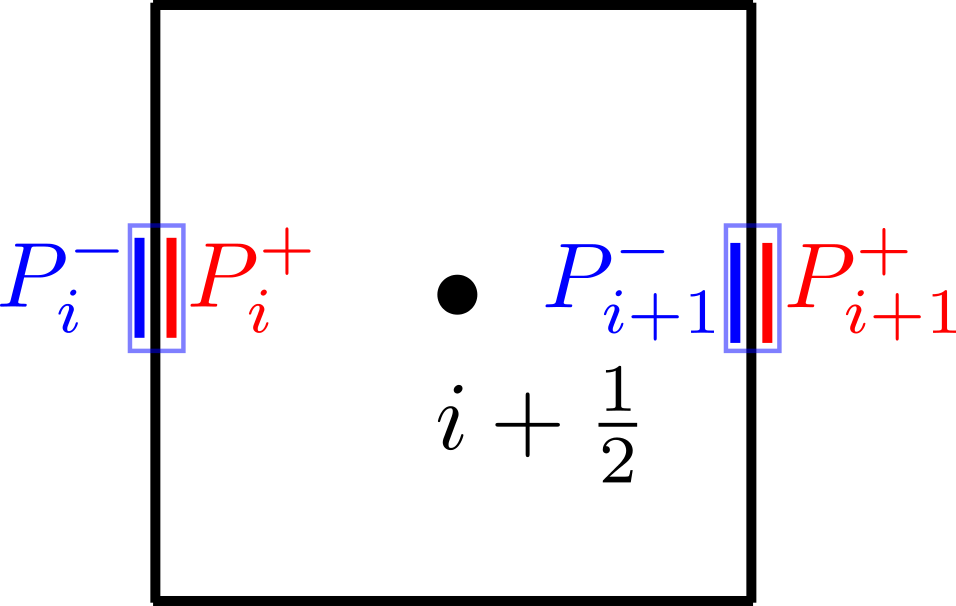
uses the Lax-Friedrichs flux for its approximate Riemann
solver, which requires as an input the maximum characteristic speed
of the physical model being solved. The Lax-Friedrichs flux is given by,